# 树
# 1 优化链表
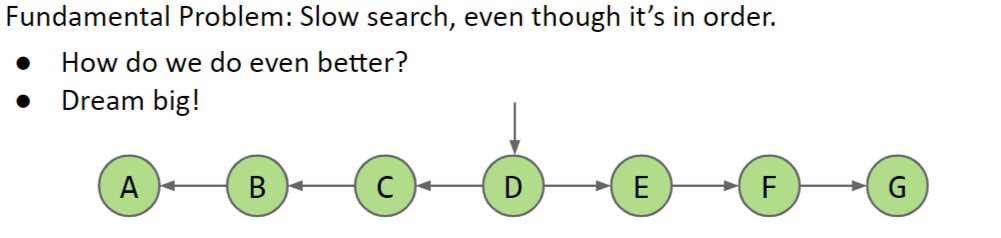
# 1 Fundamental Problem: Slow search, even though it’s in order.
- How do we do even better?
- Dream big!
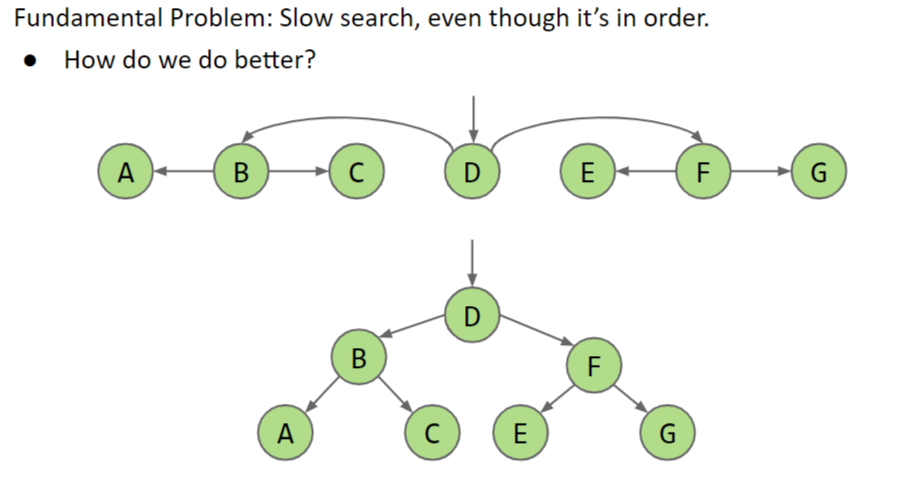
# 2 BST
# 1 search
- 与二分搜索思想相同
static BST find(BST T, Key sk) {
if (T == null)
return null;
if (sk.keyequals(T.label()))
return T;
else if (sk ≺ T.label())
return find(T.left, sk);
else
return find(T.right, sk);
}
# 2 insert
static BST insert(BST T, Key ik) {
if (T == null)
return new BST(ik);
if (ik ≺ T.label()))
T.left = insert(T.left, ik);
else if (ik ≻ T.label())
T.right = insert(T.right, ik);
return T;
}
# 3 delete :
# 3 Cases
- Deletion key has no children.
- Deletion key has one child.
- Deletion key has two children.
# 1 No children
If the node has no children, it is a leaf, and we can just delete its parent pointer and the node will eventually be swept away by the garbage collector.
# 2 One child
If the node only has one child, we know that the child maintains the BST property with the parent of the node because the property is recursive to the right and left subtrees. Therefore, we can just reassign the parent's child pointer to the node's child and the node will eventually be garbage collected.
# 3 Two children
If the node has two children, the process becomes a little more complicated because we can't just assign one of the children to be the new root. This might break the BST property.
Instead, we choose a new node to replace the deleted one.
We know that the new node must:
- be > than everything in left subtree.
- be < than everything right subtree.
In the below tree, we show which nodes would satisfy these requirements given that we are trying to delete the dog node.
To find these nodes, you can just take the right-most node in the left subtree or the left-most node in the right subtree.
Then, we replace the dog node with either cat or elf and then remove the old cat or elf node.
This is called Hibbard deletion, and it gloriously maintains the BST property amidst a deletion.
#
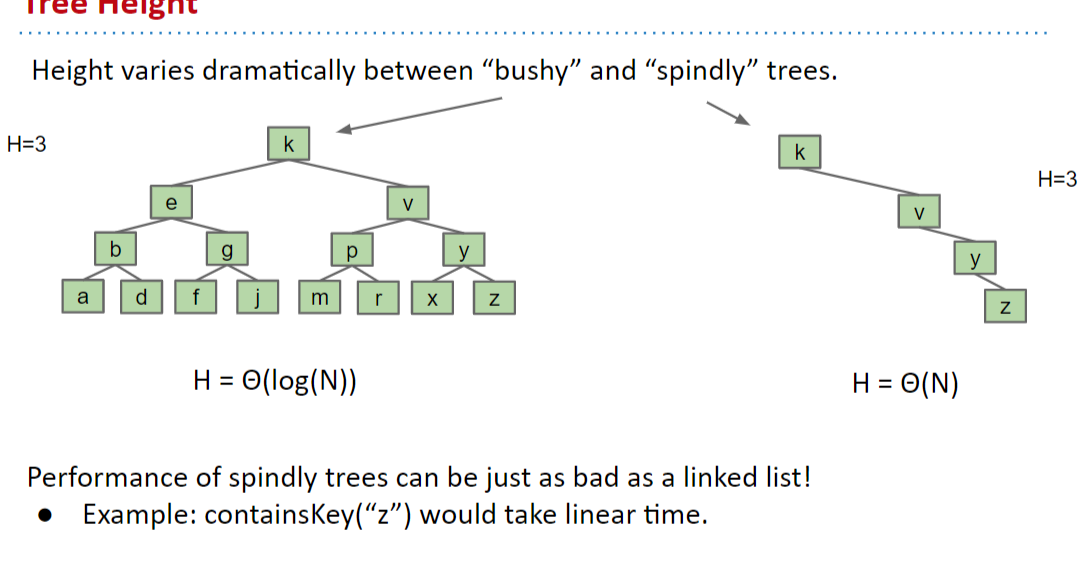
# 4 performance
- Height varies dramatically between “bushy” and “spindly” trees.
- 取决于树的 密度? 疏(bad) : 密(good);
# 3 summary
# 1 Binary search trees: Efficient data structures for supporting insertion and search.
Operations on “Bushy” BSTs are logarithmic time.
Insertion of random data yields a bushy BST.
- On random data, order of growth for get/put operations is logarithmic.
# 2 Performance issues:
“Spindly” trees have linear performance.
Hibbard deletion results in order of growth that is sqrt(N).
- Nobody knows how to do better on simple BSTs. Can improve to log(N) by having Hibbard Deletion that randomly picks successor vs. predecessor.