# Hash

# 1 尝试

# 1 缺点： 表太大，浪费内存

public class DataIndexedIntegerSet {
    private boolean[] present;

    public DataIndexedIntegerSet() {
        present = new boolean[2000000000];
    }

    public void add(int x) {
        present[i] = true;
    }

    public boolean contains(int x) {
        return present[i];
    }

# 2 散列函数

• 散列表的基本思想，是采用一个桶数组 A[]，然后借助一个散列函数 h()，根据条目(key, value) 的关键码 key 直接得到其对应的桶单元编号 A[h(key)]，从而快速地完成访问与修改。然而遗憾的是， 很难保证不同关键码所对应的桶编号不致冲突

# 1 将关键码 key 映射为一个整数 h(key) ∈ [0. .N-1]，并将对应的条目存放至第 h(key)号桶内，其中 N 为桶数组的容量。

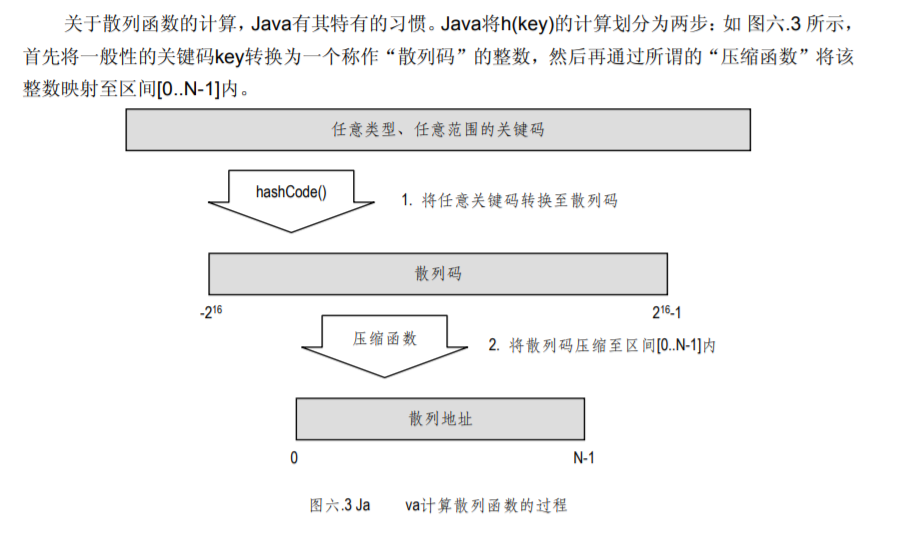
# 2 散列码

• 如上所言，Java 可以帮助我们将任意类型的关键码 key 转换为一个整数，称作 key 的散列码 （Hash code）。请注意，散列码距离我们最终所需的散列地址还有很大距离⎯⎯它不见得落在区间 [0..N-1]内，甚至不见得是正的整数。不过这并不要紧，在这一阶段我们最关心的是：各关键码的散 列码之间，应尽可能地减少冲突。显然，要是在这一阶段就发生冲突，后面的冲突就无法避免。此 外，从判等器的判等效果来看，散列码必须与关键码对象相互一致

• hashCode()方法的返回值是一个 32 位 int 型整 数。通常，这一方法会被 Java 中的每个对象继承。实际上，这一默认 hashCode()方法所返回的不 过就是对象在内存中的存储地址。

• 这种散列码的转换办法对字符串型关键码就极不适用。若两个字符串对象完全相等，本 应该将它们转换为同一散列码，但由于它们的内存地址不同，由 hashCode()得到的散列码将绝对不会一样。实际上，在实现 String 类时，Java 已经将 Object 类的 hashCode()方法改写为一种更加适 宜于字符串关键码的方法。如果你需要在映射结构中使用特定类的关键码，那么最好也按照前面所 讲的原则，重写出更为适宜的专用 hashCode()方法。

# 3 压缩函数

#

• 至此，我们已经掌握了将不同对象转化为散列码的办法，但这还不够。如果直接将散列码作为 桶数组的单元地址，则桶的容量将达到 2的32次幂 = 4 G，对于大多数应用问题来说，即使能够提供如此大 的空间，其利用率也往往极低。因此，有必要将散列码进一步压缩至我们希望的[0..N-1]区间内。

# 2 冲突处理（Handing collisions）

# 1 冲突的普遍性⎯⎯生日悖论

# 2 分离链（Separate chaining）

• 解决冲突最直截了当的一种办法，就是将所有相互冲突的条目组成一个（小规模的）映射结构， 存放在它们共同对应的桶单元中。
• 也就是说，桶单元A[i]对应于映射结构Mi，其中存放所有满足h(key) = i 的条目(key, value)。

# 3 线性探测（Linear probing）

• 采用开放定址策略，最简单的一种形式就是线性探测法。
• 在执行 put(key, value )操 作时，倘若发现桶单元 A[h(key)]已经被占用，则转而尝试桶单元 A[h(key)+1]。
• 要是 A[h(key)+1]也 被占用了，就继续尝试 A[h(key)+2]。
• 如果还有冲突，则继续尝试 A[h(key)+3]。
• 如此不断地进行尝 试，直到发现一个可以利用的桶单元。
• 当然，为了保证桶地址的合法性，第 i 次尝试的桶单元应该 为 A[(h(key)+i) mod N]，i = 1, 2, 3, …。 按照这种办法，被尝试的桶单元地址构成一个线性等差数列，故由此得名。

# 3 set && map

# 1 set

public class DataIndexedIntegerSet {
    private boolean[] present;

    public DataIndexedIntegerSet() {
        present = new boolean[2000000000];
    }

    public void add(int x) {
        present[i] = true;
    }

    public boolean contains(int x) {
        return present[i];
    }

# 2 map

public class hashCodeST<Key, Value >{
    private N;

    private hashCodesearch<Key, Value>[] st;
    public hashCode(){
        this(997);
    }

    public hashCodeST(int M){
        this.M= M;
        st = (hashCodesearch<Key, Value[]) new hashCode();
        for(int i = 0; i<M; i++){
            st[i] = new hashCodesearch();
        }
    }

    private int hash(Key key){
        return (key.hashCode() & Ox7ffffffff)%M;
    }

    public Value get(Key key){
        // return (Value)  st[hash(key)].get(key);
        int  i = hash(key);
        for(Node x = st[i]; x!= null; x= x.next){
            if(key.equals(x.key))  return (Value) x.val;
        }
        return null;
    }

    public put(Key key, Value val){
        // st[hash(key)].put(key, val);

        int  i =hash(key);
        for(Node x = st[i]; x !=null; x= x.next){
            if(key.equals(x.key)){
                x.val = val;
                return;
            }
        }
        st[i] = new Node(key, val, st[i]);
    }
}

# 4 无序词典与有序词典

# 1 无序词典

• 散列的思想不仅可以用以实现映射ADT，也可以用来实现无序词典ADT。具体来说，我们还是 使用一个桶数组A[]，其中的每个桶分别对应于一组关键码相等（或者说相互冲突）的条目；我们采 用分离链策略，将每一组这样的条目再组织为一个子词典，存放在对应的桶中。实际上，只要装填 因子足够小，并选取适当的散列函数以保证各条目的均匀分布，则每个这类子词典的规模都不会很 大，因此无需采用复杂的结构加以实现⎯⎯比如。

# 2有序词典

• 前面曾提到，基于无序列表实现的词典结构非常适用于解决网络访问日志之类的应用问题，这 类问题的共同特点是：插入操作频繁，查找、删除操作却极少进行。另外一些问题则正好相反，它们要求频繁地进行查询，但插入、删除操作相对更少，这方面的例子包括在线电话簿、订票系统等。

• 在对系统响应速度要求极高的场合（比如各种实时处理或服务系统），散列表的上述不足往往是 致命的。比如在航天飞机的控制系统中，如果查找算法的效率时高时低，那么一旦出现查找的最坏 情况，后果将不堪设想

• 只要在关键码之间定义有某一全序关系，我们就可以将词典中的条目组织为一个有序向量S，。这里之所以选择向量而不是列表，是因为正如我们马上就要看到的，前者能够支持对词典的快速查找。

• 二分查找 尽管有序查找表的更新效率不高，但由此却可以将查找效率提高至 O(logn)。 我们采用通常的习惯，通过条目的秩来表示它们之间的全序关系